News
- 25.09.2018: The exam review for the second exam will take place this Wednesday, September 26th, from 11:00-12:00 in lecture hall AH VI. Please bring your BlueCard.
- 20.09.18: The second exam for Model Checking takes place this Friday, September 21st, at 14:00 in AH IV. You are allowed to bring your copy of the slides and the Principles of Model Checking book. No own notes are allowed.
- 05.09.2018: The correction of the first exam has been completed. Please find your result in the L2P. The review for the exam will take place on Friday, 07.09, in room 5056. To prevent long queues, we partitioned the group based on their matriculation number as shown below. Please bring your BlueCard.
Matriculation number Time < 345 000 09:15 to 10:15 > 345 000 10:15 to 11:15 - 23.08.18: Fixed a path in the solution of task 3(b) of sheet 4.
- 21.08.18: We uploaded the solution for the old exam.
- 20.08.18: Fixed a minor typo in the solution of sheet 5.
- 02.08.18: We uploaded an old exam as preparation for the exam.
- 16.07.18: There will be a Q&A session on Thursday, 23.8., from 9:30 to 12:30 in AH IV. Please send us your questions before the question session via mail.
- 06.07.18: two typo’s in the slides of lecture 19 have been fixed
- 27.06.18: We updated the sample solution of exercise sheet 8 to account for two missing transitions in task 1(c).
- 12.06.18: We updated the seventh exercise sheet to fix a typo in task 4(b).
- 29.05.18: Since we have not given the formal GNBA to NBA transformation in the lecture, we included it on exercise sheet 5.
- 18.05.18: Due to an unfortunate oversight, we updated the fourth exercise sheet to repair task 1 (again). We apologize for any inconveniences.
- 16.05.18: The period for the exam registration ends this Friday, 18th May. Make sure to register before this deadline.
- 16.05.18: We updated the fourth exercise sheet to fix a typo in task 3.
- 14.05.18: We updated the fourth exercise sheet to repair task 1.
- 03.05.18: We updated the second exercise sheet to make task 1 more precise.
- 30.04.18: The poll revealed that there are too many clashes when changing the date of the first exam, so we will stick to the old date (31 August).
- 23.04.18: The first exercise sheet is online.
- 20.04.18: We opened a poll in L2P to determine whether we need to shift the date of the first exam. Please indicate until next Wednesday whether you are available in specific time slots.
- 16.04.18: Please register to the L2P room for the lecture via Campus Office. Not only will announcements reach you more quickly, but questions concerning the lectures and exercises can be posted in the L2P forum.
- 13.04.18: We changed the room for the exercise class to AH II.
- 27.03.18: Adapted the dates for the first lectures and added information about the exams.
- 02.03.18: We are online.
Schedule
| Type | Day | Time | Hall | Start | Lecturer |
|---|---|---|---|---|---|
| Lecture | Tue | 08:30 – 10:00 | AH II | 24.04. | Katoen |
| Fri | 10:15 – 11:45 | AH V | 13.04. | Katoen | |
| Exercise | Mon | 12:15 – 13:45 | AH II | 30.04. | Hensel / Volk |
Slides
| No. | Date | Topic | Slides |
|---|---|---|---|
| 1 | 13.04. | Introduction | mc2018_lec1 |
| 2 | 20.04. | Transition systems | mc2018_lec2 |
| 3 | 24.04. | Concurrency | mc2018_lec3 |
| 4 | 27.04. | Channel systems | mc2018_lec4 |
| 5 | 04.05. | Linear-time properties | mc2018_lec5 |
| 6 | 08.05. | Safety and Liveness | mc2018_lec6 |
| 7 | 11.05. | Fairness | mc2018_lec7 |
| 8 | 15.05. | Verifying regular safety properties | mc2018_lec8 |
| 9 | 18.05. | Büchi automata (1) | mc2018_lec9 |
| 10 | 29.05. | Büchi automata (2) | |
| 11 | 01.06. | Verifying omega-regular properties | mc2018_lec11 |
| 12 | 05.06. | Linear temporal logic | mc2018_lec12 |
| 13 | 08.06. | Expansion law, fairness, PNF | mc2018_lec13 |
| 14 | 12.06 | LTL model checking (1) | mc2018_l14+15 |
| 15 | 15.06 | LTL model checking (2) | |
| 16 | 19.06 | Complexity of LTL model checking | mc2018_l16 |
| 17 | 22.06 | Computation tree logic | mc2018_l17 |
| 18 | 26.06 | LTL versus CTL | mc2018_l18 |
| 19 | 29.06 | CTL model checking | mc2018_l19 |
| 20 | 03.07 | CTL and fairness | mc2018_l20 |
| 21 | 06.07 | CTL+ and CTL* | mc2018_l21 |
| 22 | 10.07 | Bisimulation and CTL* equivalence | mc2018_l22 |
Exercises
| No. | Handed Out On | Date Due | Exercise Sheet | Solution |
| 1 | 23.04. | 30.04 | ex01 | sol01 |
| 2 | 30.04. | 07.05 | ex02 | sol02 |
| 3 | 07.05. | 14.05 | ex03 | sol03 |
| 4 | 14.05. | 28.05. | ex04 | sol04 |
| 5 | 28.05. | 04.06. | ex05 | sol05 |
| 6 | 05.06. | 11.06. | ex06 | sol06 |
| 7 | 11.06. | 18.06. | ex07 | sol07 |
| 8 | 18.06. | 25.06. | ex08 | sol08 |
| 9 | 25.06. | 02.07 | ex09 | sol09 |
| 10 | 02.07. | 09.07 | ex10 | sol10 |
| 11 | 09.07. | 16.07. | ex11 | sol11 |
| old exam | sol_exam |
Exam
| Date | Time | Location | |
|---|---|---|---|
| First exam | Fri, 31. August 2018 | 14:00 – 16:00 | Großer Hörsaal AM |
| Re-exam | Fri, 21. September, 2018 | 14:00 – 16:00 | AH IV |
You are allowed to bring your copy of the slides and the Principles of Model Checking book. No own notes are allowed.
Motivation
In 2008, the ACM awarded the prestigious Turing Award – the Nobel Prize in Computer Science – to the pioneers of Model Checking: Ed Clarke, Allen Emerson, and Joseph Sifakis.



Why?
Because model checking has evolved in the last twenty-five years into a widely used verification and debugging technique for both software and hardware.
It is used (and further developed) by companies and institutes such as IBM, Intel, NASA, Cadence, Microsoft, and Siemens, to mention a few, and has culminated in a series of mostly freely downloadable software tools that allow the automated verification of, for instance, C#-programs or combinational hardware circuits.
Subtle errors, for instance due to multi-threading, that remain undiscovered using simulation or peer reviewing can potentially be revealed using model checking. Model checking is thus an effective technique to expose potential design errors and improve software and hardware reliability.
But how does it work, that is, what are its underlying principles?
That’s exactly the focus of this lecture series!
We will show that model checking is based on well-known paradigms from automata theory, graph algorithms, logic, and data structures. Its complexity is analyzed using standard techniques from complexity theory.
Contents of the Lecture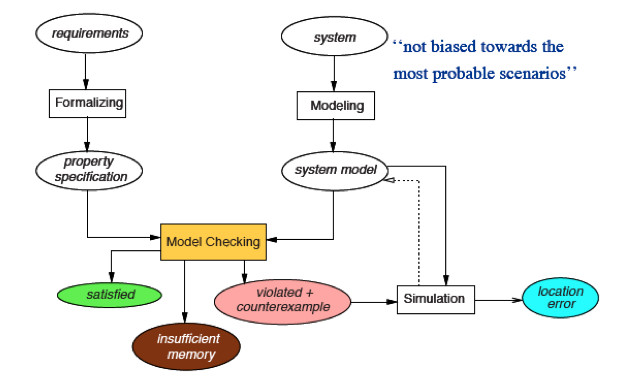
Model checking is based on, well, checking models. So, we first start by explaining what models are, and will make clear that so-called labeled transition systems, a model that is akin to automata, are suitable for modeling sequential, as well as multi-threading programs.
This is followed by a detailed study on various classes of system properties such as safety, liveness, and fairness. It will be shown how finite automata as well as variants thereof that accept infinite words are suitable for verifying regular properties.
The linear-time and branching time temporal logics LTL and CTL are then introduced and compared. Model checking algorithms for these logics together with detailed complexity considerations are covered.
Finally, abstraction techniques based on bisimulation and simulation relations are covered. These techniques are at key techniques to combat the state explosion problem.
Prerequisites
We expect students to have some basic knowledge in:
- Automata Theory
- Mathematical Logic
- Discrete Mathematics
- Complexity Theory
- Algorithms and Data Structures
The course book (see below) will contain a summary of the issues in these areas that are relevant to this lecture series. We believe that this course is also well-suited for students in electrical engineeering and mathematics.
Materials
The lectures and all materials are in english. The slides will be made available via this webpage during the course.
The course is based on:
Principles of Model Checking
by Christel Baier and Joost-Pieter Katoen
MIT Press, 2008.

An errata document to the book may be found here.
It is possible to buy a book (about 40 euros), but there is no need to do so as there are various copies of the book available at the CS library.
The course will basically cover Chapters 1 through 7 (upto section 7.3).
Additional literature:
- E.M. Clarke, O. Grumberg, D.A. Peled: Model Checking, MIT Press, 1999
- M. Huth and M.D. Ryan: Logic in Computer Science – Modelling and Reasoning about Systems, Cambridge University Press, 2nd edition, 2004
- K. Schneider: Verification of Reactive Systems, Springer-Verlag, Texts in Theoretical Computer Science. An EATCS Series, 2004