On February 8, 2019, I have defended my PhD thesis titled Advanced Weakest Precondition Calculi for Probabilistic Programs. You can access a PDF file of my thesis by clicking the cover below.

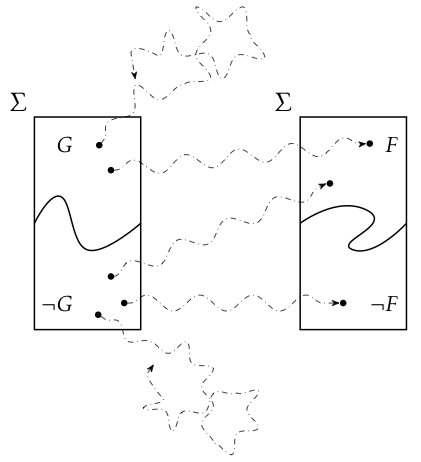
The thesis is structured into three parts. Part I gives a comprehensive introduction to Dijkstra’s weakest-precondition-style reasoning for deterministic programs at the level of predicates. Thereafter, we gradually advance from the level of predicates to reasoning about quantities. Finally, we give a comprehensive introduction to weakest preexpectation reasoning for probabilistic programs in the style of McIver & Morgan which builds on earlier work of Kozen.
Additionally, we study in Part I different forms of termination of probabilistic programs. We survey existing proof rules for proving almost-sure termination (i.e. termination with probability 1) as well as positive almost-sure termination (i.e. termination within finite expected runtime) and present a new proof rule for almost-sure termination.
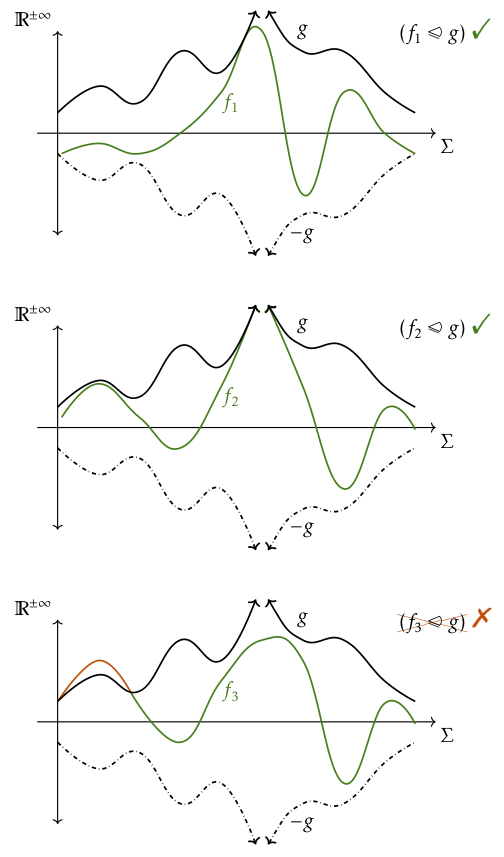
In Part II, we then develop three more advanced weakest-precondition-style calculi for quantitative reasoning about probabilistic programs. Concretely, those calculi enable reasoning about
As with Dijkstra’s calculus, our calculi are defined inductively on the program structure and thus allow for compositional reasoning on source code level. Both in Part I and II we put a special emphasis on (mostly inductive) proof rules for reasoning about loops.
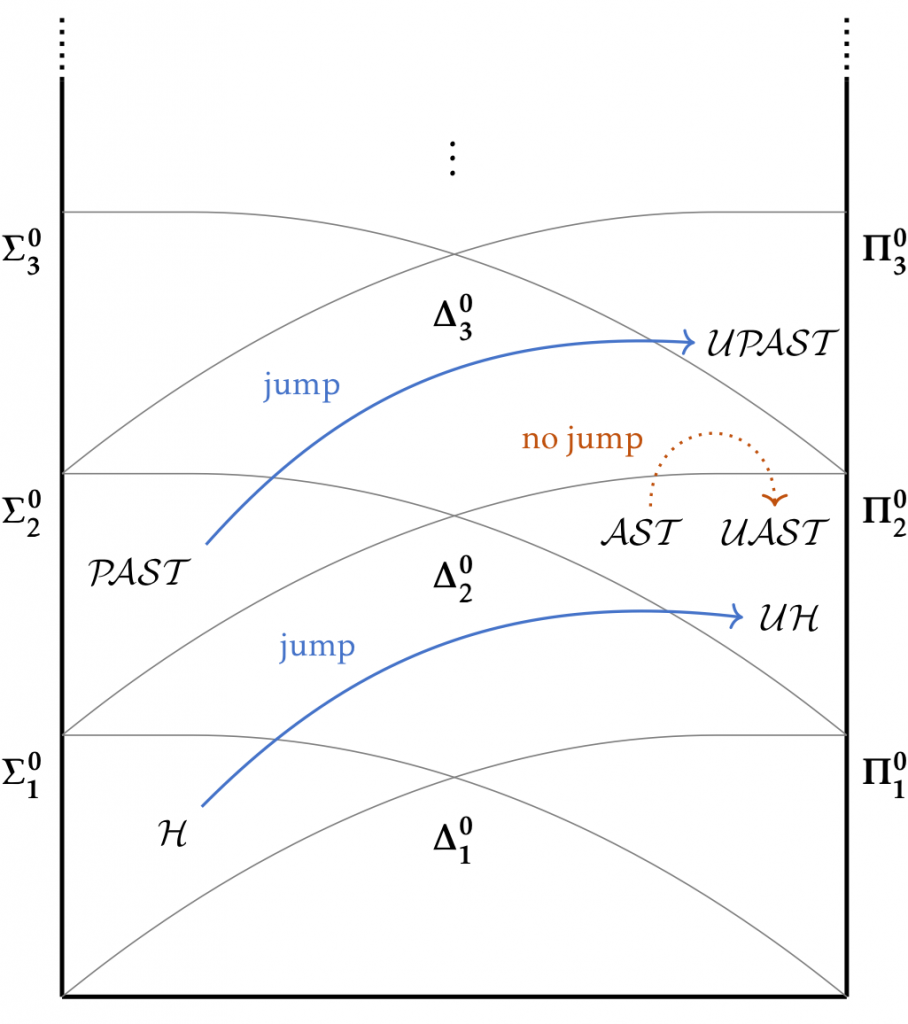
In Part III, we study the computational hardness of reasoning about probabilistic programs. This hardness is independent from the employed analysis technique and hence inherent to the considered analysis problems themselves.
All our results are presented in terms of levels of the arithmetical hierarchy, for which the analysis problems we consider are complete.
Concretely, we study the hardness of
- computing and approximating expected values and (co)variances, and
- deciding termination of probabilistic programs, in particular almost-sure termination and positive almost-sure termination.
The cover art for my thesis was designed by my cousin Benoît Texier and presents an artistic depiction of the arithmetical hierarchy. The thesis is published online via RWTH Aachen’s University Library.